Terminal Velocity in a Vacuum
It is commonly claimed that an object dropped in a vacuum will continue to accelerate indefinitely, reaching arbitrarily high speeds. In fact, even in a vacuum, a falling object has a maximum speed it can reach. In essence, this is the terminal velocity in a vacuum.
Reflecting on the Reflection Principle
From finance to route planning, the reflection principle is an incredibly versatile technique, capable of transforming seemingly fiendish problems into elegant systems. In this post, I walk through three example applications of the principle.
Efficient Calculation of Efficient Frontiers
The efficient frontier is a ubiquitous tool in quantative finance, yet it is often calculated using incredibly inefficient methods. Can we do better using a healthy helping of analysis and linear algebra.
A Polish Approach to Countdown
The Countdown numbers game is notoriously fiendish. That said, with the right computational tricks, it can be solved using only basic coding abilities.
The Look-and-Say Sequence: A Tribute to John Conway
One week ago today, we lost one of the most inspirational mathematicians of this generation. In this post, we take a brief look at the incredible legacy that John Conway left behind. On top of that we will discuss one of the many problems he tackled during his career; one that, to this day, occupies a special place in my heart. We close by discussing an intriguing puzzle that I am yet to find a solution to—can you?
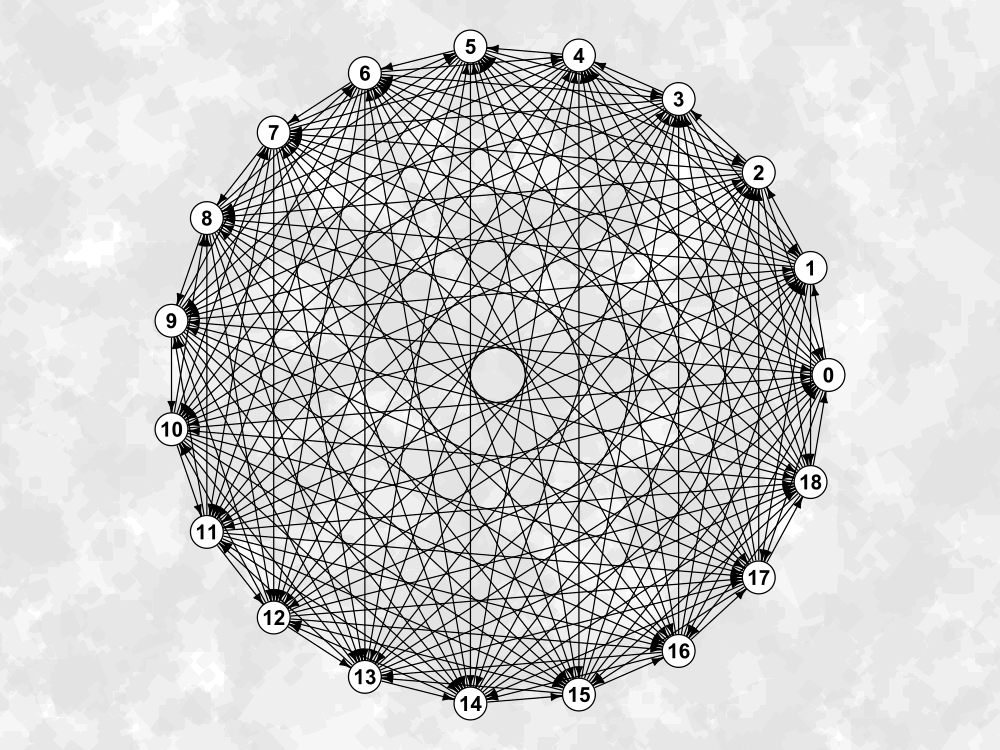
Paradoxical Tournaments
Deciding the winner of a round-robin tournament is no simple task. The most naïve approach can easily be faltered by the existence of $k$-paradoxical tournaments. But what are these tournaments and what do we know about them? There is surprisingly little discussion on the topic and so, in this post, I plan to collate various pieces of knowledge on the subject into one succinct guide.
Integration Tricks using the Exponential Distribution
Not all integrals are created equally. In this post we look at a particular class of integrals which can be highly troublesome to evaluate. Thankfully, probability theory provides us with a framework that allows us to avoid the standard method of evaluation and by doing so makes our working far less error-prone.