I understand why people use Excel. I really do.
As a user of Python and R, amongst several other programming languages, I often find it frustrating that so many people gravitate towards Excel regardless of the nature of the problem they are trying to solve. For simple accounting, visualisation, and data entry I think that Excel is the perfect tool. As the scale and complexity of applications begin to grow, however, it starts to feel that the comfort people find in Excel ends up being more of a burden than a blessing.
In my work, I have seen many complicated and expansive software tools productionised using Excel. On top of this, the lack of portablity between Excel versions, the difficulty of maintaining and documenting such applications, and the inivitable performance limits that a user runs into, have repeatedly made themselves clear. All of this hassle makes me wonder whether it would just be easier for the developers of these products to learn a new, more suitable toolset. It may take a while to learn, say Python, to a competent level, but after seeing the frustration Excel can cause, maybe this is a worthy investment for the long-run.
I say this and yet, I’ve never truely given Excel a full evaluation; I’ve never attempted to throw some of the more complicated projects I come across at the program and see how it copes. This is going to change, however. So that I can feel entirely justified in nudging developers away from Excel towards more formal toolsets, I have decided to start a new series in which I aim to push Excel to its limits to see if (more likely, when) it breaks and how the development of such complicated applications manifests itself.
In this first installment, we will look at a mathematical puzzle known as the peaceable queens problem. Can Excel solve this problem? If so, how monsterous will the solution become? Read on to find out.
The Peaceable Queens Problem
The peaceable queens problem is relatively obscure in the world of mathematics, but presents an interesting challenge just about suitable for solving in Excel. It concerns a chessboard of dimensions $m\times n$ where $m,n$ are arbritary positive integers. The goal of the problem is to find the maximum integer $z$ such that $z$ black queens and $z$ white queens can coexist on the chessboard without attacking each other.
For example, in the case where $m,n=4$ we have a $4\times4$ chessboard. The diagram below first shows an invalid (non-peaceable) solution. This is followed by a valid solution (all queens coexist) that is not optimal (at least one queen of each colour can be added whilst maintaining peace). The final board shows one of many optimal solutions featuring two queens of each colour. You can try as hard as you’d like to find an arrangement with three queens of each colour, but trust me, you’ll be searching for a while!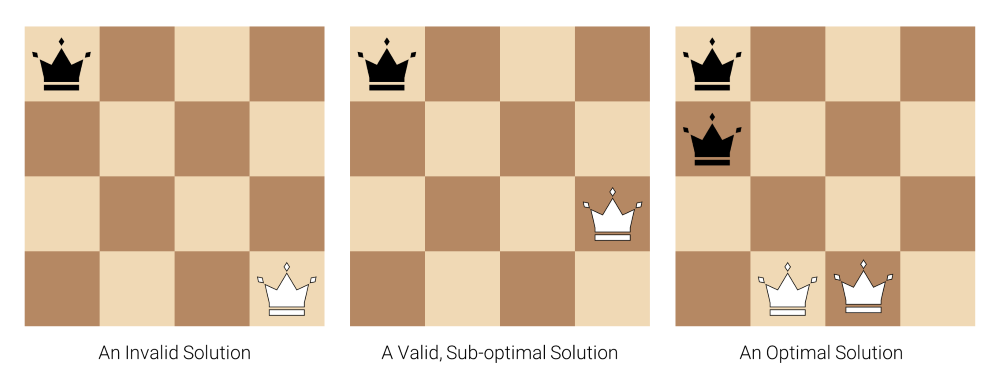
Note that we require any solution to have the same number of black and white queens. Hence, even if we can add more queens of just one colour to an existing solution, this has no value to us.
The above gives a solution (though admittedly, not a proven one) for a specific case. What about general $m,n$? Before we create an Excel spreadsheet to solve this problem, let’s see what mathematicians have found out using general methods.
The State of the Art
I came across this problem when looking at the Online Encyclopedia of Integer Sequences (OEIS). This site consists of an immense collection of sequences of integers (e.g. the Fibonacci sequence, the prime numbers). The 250,000th of which just so happens to be the sequence of optimal values of $z$ in the peaceable queens problem for square chessboards of increasing sizes. For example, the fourth entry in the sequence corresponds to the chessboard of size $4\times4$ and so has a value of $2$ as we saw above.
The earliest known reference to this problem was by Stephen Ainley in his 1977 book of mathematical puzzles. Ainley found layouts for square chessboards up to size $30\times30$, only one of which ($27\times27$) has since been improved upon. There is reason to believe that many of these solutions are indeed optimal, yet we have only proved this for results up to $15\times15$. Therefore if we can solve the problem for chessboards of size anywhere near $15\times15$ we will have achieved a lot.
Although we do not currently have optimality proofs for $n>16$, reasonable lower and upper bounds do exist. You can read more about these in the [sequence]’s(https://oeis.org/A250000) comments section.
A Mathematical Formulation
Before we jump into our Excel-based solution, we will have to reframe the problem in a mathematical setting. Specifically, we can describe the problem as an Integer Programming Problem. It’s not worth sweating over the details of this and so if you don’t care for the maths, you can skip the rest of this section. The important takeaway is that the problem can be thought of as this special integer programming formulation, the likes of which Excel is equipped to solve.
Specifically, for $i\in[m]$, $j\in[n]$ we let $b_{ij}$, $w_{ij}$ represent be the binary indictors of whether there is a black or white queen in the square $(i,j)$, respectively. Our goal then becomes to maximise
$$z := \sum_{i=1}^m\sum_{j=1}^n b_{ij}$$
subject to
$$\sum_{i=1}^m\sum_{j=1}^n b_{ij} = \sum_{i=1}^m\sum_{j=1}^n w_{ij}$$
and
$$b_{i_1j_1}+w_{i_2j_2}\leq 1 \quad \forall ((i_1, j_1), (i_2, j_2))\in M$$
where $M$ is the set of all ordered pairs of squares that share a line (row, column or diagonal) of the board.
It is clear to see that this formulation involves $2mn$ variables. Counting the number of constraints is more challenging. We will have $2mn$ binary constraints plus one more to enforce an equal number of black and white queens. Then we are left with constraints for peacability, of which there will be $|M|$. For each $(i_1, j_1)\in[m]\times[n]$ there are $(m-1) + (n-1) + 2(\text{min}(m, n) - 1)$ squares $(i_2, j_2)\in[m]\times[n]$ that share a line with $(i_1, j_1)$ (you can just count them; don’t overthink it) and so |M| = $mn(m-1 + n-1 + 2(\text{min}(m, n) - 1))$. It is clear that this dominates the number of constraints and so overall we have $\mathcal{O}(mn\text{max}(m, n))$ constraints. For $m=n$ we see that the number of constraints is $\mathcal{O}(n^3)$—not great!
This formulation turns out to be sub-optimal, but for our purposes it will do. See here for a more detailed analysis of the problem.
Excel Abuse
You can download the final spreadsheet from this link. Note that you will need to enable content as the worksheet depends on macros.
With the maths out of the way, we can move onto solving the problem using Excel. As suggested above, Excel has a built-in add-on for solving many types of optimisation problems such as integer programming problems. Since we can formulate the peaceable queens problem in this way, we’re in a good position to solve it. The only issue is that Excel requires a lot of structural and formula overhead to start the solver (i.e. we must populate the worksheet with a lot of relevant information). In my first draft I did this by hand for the $3\times3$ case, but this takes a long time so is not suitable for a general solution. Instead we can leverage VBA, a scripting language for controlling Excel, to automatically generate such content.
Creating a Solution
I began by creating a user interface consisting of two dimension inputs, two buttons, and a static colour key.

The dimension inputs have data validation restricting values to be integers in the range 2–3 (more on this later). Once these are set to the desired values, clicking the ‘Solve Problem’ button will populate the sheet with the information Excel’s solver requires and then begin solving the problem. After a few seconds a dialog box will appear to notify the user that a solution has been obtained.
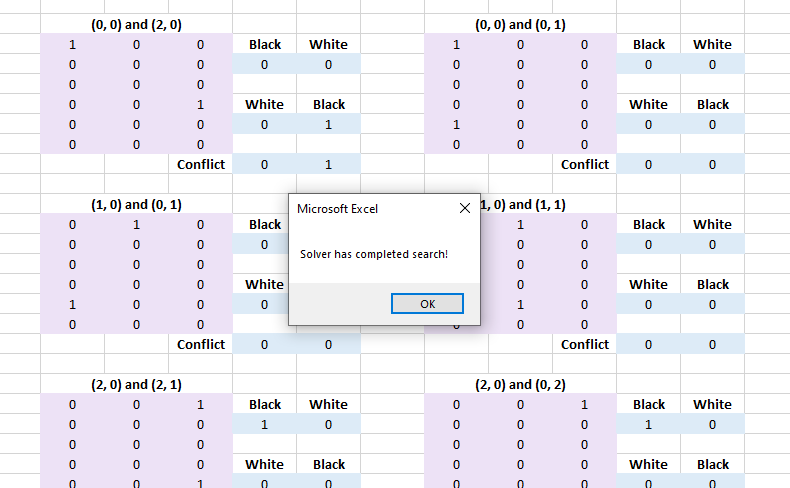
Note that when a solution is found it has also been proven to be optimal. There may be other valid solutions but they will have at most the same number of queens.
A solution can then be read off from the green boxes, the orange cells showing the optimal value of $z$ found. The box titled ‘Blacks’ corresponds to the positions of the black queens (a square has value one if and only if there is a black queen there) and likewise for the ‘Whites’.

We have a solution…for the $3\times3$ case that is. Unfortunately, the built-in Excel solver does not scale well. Due to this, Microsoft have put limits on the number of variables (100) and constraints (200) you are able to use for an optimisation problem. For the $3 \times 3$ and smaller cases, we do not surpass these limits yet for $3 \times 4$ and larger we do. Therefore, although our solution works in theory, it has little us in practice.
Going Further
The limitations of the built-in solver are rather disappointing. Thankfully, a workaround comes in the form of FrontlineSolvers‘ suite of 3rd-party Excel solver plugins. Unfortunately, this software is equipped hefty price tag of a few thousand dollars. Luckily for us, there is a free 15-day trial. I signed up for this (no card required), installed the software, and let it loose on some larger problems. This raised the size of the largest possible board to around $10\times10$. This is still not limited by the implemented approach but rather that the trial version has its own (though admittedly, large) variable and constraint limits too. My back-of-the-envelope calculation suggests that the full version of this solver (with no limits and access to solving algorithms optimised for sparse systems) could result in solutions for boards up to $12\times12$ and perhaps $13\times13$ with some patience. This is incredible considering that no approach to the problem is yet to surpass $15\times15$.
Adapting the workbook to use FrontlineSolvers’ solver is simple. First install the trial version of the solver. Then open the existing workbook, disable protection and remove data validation from the dimension cells. Click the ‘Solve Problem’ button as before. This populate the spreadsheet but will not find a solution (since this surpasses the default solver’s limits). The sheet will now be protected so disable this again. Navigate to the ‘AnalyticSolver’ tab in the top ribbon and select ‘Model’. This will open a sidebar, and selecting the green play button will solve the problem.
The largest solution I found was for the $10\times10$ board. This took a few hours of my computer’s intense labour to discover and subsequently prove optimality. Thankfully there is no NSPCMP (National Society for the Prevention of Cruelty to Microsoft Products) so I got away with this abuse. The resulting layout is as follows.

Conclusion
I don’t want this post to drag on so I will refrain from offering a solution using a more appropriate tool such as Python or R for comparison. Note though, that even though this solution does technically work, it is clunkly, ugly, and would require several thousands of dollars worth of spare cash to implement asl a permanent solution (though why you’d have a regular need for find peaceable arrangements of queens, I do not know). An equivalent tool using a formal language could easily be much faster, portable, and—most importantly—completely free for any scale your computer can handle.
Solving this problem was fun but the conclusion only confirms my initial beliefs—if the problem is this complex, save Excel the abuse.